Lesson 15 Slides | Fishtank Learning

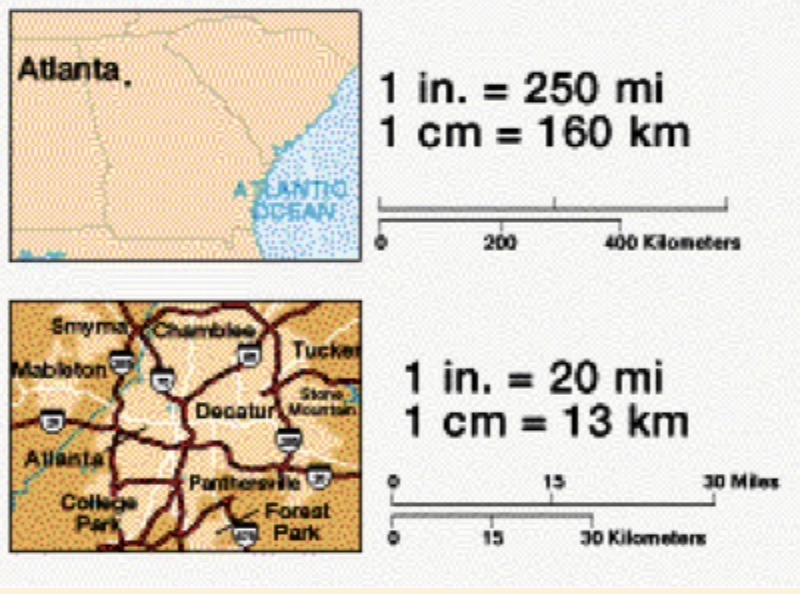Anchor Problems - Problem 1

Cory is looking at a digital trail map of a local park. On the map, a trail segment is 2 inches long. The scale of the map says: 1 inch = 200 feet.

a. How long is this trail segment in real life? Show your reasoning.

b. Cory zooms to 160% on the digital map to see more detail.

What is the new scale of the map after zooming in?
How long will the same trail segment appear in the zoomed-in image?

Purpose

This problem engages students in reasoning about scale and the impact of different scales in a digital mapping context. Students interpret and apply a scale to convert map measurements to an actual distance and consider how changing the display by zooming in affects the scale and the representation on the map. The task provides simple numbers that keep the focus on proportional reasoning and conceptual understanding.

Facilitation Guidance

Launch the problem by projecting a digital map and investigating the zoom feature with the class. Ask them to notice and wonder about the scale bar and labels, the image itself and the level of detail of the map. Prompt students to consider the benefit of different zooms, such as using a zoomed-out map to look at an overview for a trip versus a zoomed-in version to actually navigate each turn. Ask some of the following questions for partners to consider and discuss:
- Why might zooming in or out change what you see?
- How does zooming change the scale? Be specific.
- What patterns do you notice when the map is enlarged?
Have students work with a partner to calculate the real-world length of the trail and analyze the effect of zooming on the map scale. Circulate to observe strategies: some students may multiply directly by the scale, while others may use tables, equations, proportions or other methods. Encourage students to reason quantitatively about how a 160% zoom affects the scale by asking some of the following questions:
- What changes, and what stays the same as Cory zooms in?
- What is the zoom of the original map?
- What happens if the zoom is changed to 75%? 200%?
- How is the zoom related to the scale and to proportionality?
Debrief the problem by inviting students to share strategies for both calculating the actual trail length and reasoning about the zoomed map. Discuss why the trail’s real-world length does not change even as the digital image grows. Ask students to extend this thinking:
- If another trail segment is 3.5 inches on the map, how long is it in real life?
- How could an equation help quickly determine the real distance for any segment?
- How does reasoning about scale help you compare distances across different maps or zoom levels?
Highlight how recognizing the structure of the problem, such as relationships between map length, scale, and zoom, supports efficiency MP.7 Look for and make use of structure. . Students can also reflect on how digital representations might mislead if scale is not considered carefully, connecting reasoning to real-world navigation and planning.
Extension: After solving, have students create their own "zoom levels" on the map. Give each group a zoom percentage (50%, 200%, 250%, etc.), and have them calculate the new scale and redraw the original 2-inch trail segment to show how it would look. Groups can hang their versions around the room so the class can "walk through the zoom levels" and compare how the same trail changes appearance.

Notes

Students may use proportional reasoning in addition to or instead of using scale factor. For example, in Part (b-ii), students could use the new scale factor calculated in Part (b-i) and the known distance to determine the length of the trail segment, or they could use the zoom factor to see how the map distance changed. Support students in seeing the similarities and differences between the zoom factor and the scale factor, and their relationship to the real-life and scaled measurements.

Anchor Problems - Problem 2

The map below shows Boston Common and Boston Public Garden. Perla walked around the outside perimeter of the Common and the Public Garden. About how far did she walk?

Purpose

In this problem, students practice precision while reasoning about acceptable variation and connecting results back to real-world contexts involving map scales. Unlike the clean proportional reasoning of the previous task, here students must decide how to measure, estimate, and apply a scale when their measurements are not exact. By working with different-sized versions of the same map, students recognize how proportional reasoning ensures consistent results across scales.

Setup

Print the map in different sizes, so that each group of students receives a map of a different size.

Facilitation Guidance

Launch the problem by displaying the map of the Boston Commons and inviting students to notice and wonder. Have students turn and talk before bringing the class together to highlight ideas about distance, measurement, the shape of the parks and the scale line. Possible follow-up questions:
- What is an estimate that is too high and an estimate that is too low?
- How might you measure the perimeter of the park?
- What tools could help you determine the actual perimeter?
- What might be tricky about solving this problem?
Give students time to work on the problem with a partner or in a group of 3, and ensure that all groups have access to the rulers, flexible measuring tools, tracing paper, etc. Ask students to first discuss what tools they will use to measure the distance on the map and be ready to explain their reasoning MP.5 Use appropriate tools strategically. . As you circulate, look and listen for how students grapple with curves (segmenting vs. continuous measures), how they anchor their conversion to the scale bar length on their specific print, and whether they keep units consistent.
Supporting Access for Students
- If students struggle with the non-regular shape perimeter, model how you might estimate with straight drawn lines, or provide string or a paper strip that students can mark with the “500 ft” segment, then “step” that unit around the perimeter.
- Collect and display student language and sketches that name how they’re using the scale bar (e.g., “one scale-unit,” “step-length,” “ticks around the edge”) to support explanations across groups.
Have groups pair up with a team that used a different print size. Ask them to compare procedures, measured perimeters, and final distances, and to discuss why results should be close even if their paper measurements and scales differ. Invite each pair to agree on a concise explanation of how they used the scale bar to convert, and what accounted for any differences. Prompt quantitative reasoning MP.2 Reason abstractly and quantitatively. and attention to prevision MP.6 Attend to precision. by asking questions like:
- What does the 500 ft correspond to on each paper? How does this change with the size of the map?
- How did each group use the scale line to scale up the perimeter to the real length?
- How did each group measure the perimeter on the map? Which methods seem most accurate? Why?
- Which maps made it easier to find a precise answer for the real length? Why?
- Why do all of the maps provide the same (or similar) approximations? What does this tell you about scale?
- What are sources of variation and how can you minimize them?
Debrief the problem by bringing the class together and spotlighting a couple of contrasting approaches for finding the perimeter on the map and calculating the actual distance in feet. Compare how different tools and methods supported precision. Support students in seeing how all of the methods used proportional reasoning. Encourage inclusive, student-to-student talk as groups compare and refine explanations CRMT Culturally Responsive Math Teaching .
- Extensions:
  - Have students print out maps of places of interest to them and find distances. For example, a student could print a map of her neighborhood and use the scale on the map to find the distance to the nearest park, the nearest store, etc.
  - Guide students to generalize their methods for calculating the actual distance for any scaled copy of any map MP.8 Look for and express regularity in repeated reasoning. .

Notes

There are many different ways that students may solve this problem using a tool of their choice: MP.5 Use appropriate tools strategically.
- Students may use rulers to determine the corresponding measure for 500 feet in the scale, find the perimeter in the map, and then use the scale to find the actual perimeter. If they use rulers, allow centimeters or inches and investigate why this doesn’t matter.
- Students may also use string or some other flexible measuring tool (such as Wikki Stix) because of the curved lengths around the Boston Common.
- Alternatively, students could define the line segment in the map scale as a single unit and calculate how many of those units fit around the perimeter using a ruler, string, tracing paper, or other tool.
Watch a video analysis of this Anchor Problem in the Unit Launch, Big Idea 2, Step 2 starting at 4:01.

Anchor Problems - Problem 3

Your school used to provide a map of the building for new students, but the original version was lost. You and your classmates are trying to draw a new one. Here’s what you remember:

The scale on the map was $$ \frac{1}{4 }$$ inch = 20 feet.
On the map, the music room and art room were 5 inches apart.
The cafeteria and the gym were $$2 \frac{1}{4 }$$ inches apart on the map.

Additionally, you measure some other distances:

The distance between the library and the auditorium is 140 feet.
The distance from the main office to the cafeteria is 350 feet.

a. Brainstorm mathematical questions that you could answer with the information provided.

b. Select two mathematical questions to answer from your list and solve them using proportional reasoning.

c. It takes about 140 steps to walk from the bus drop-off to the science wing. If each step is roughly 2.5 feet, about how far apart are these locations in real life? How far apart would they be on the map?

Purpose

This problem invites students to generate and solve mathematical questions using a fractional map scale, building on their foundation of proportional reasoning with maps from the previous two Anchor Problems. By translating between scaled map measurements, actual distances, and approximate number of steps, students practice sense-making and deepen their understanding of how quantities in scales relate, helping them avoid the common mistake of confusing which operation to use (multiplication or division) with a scale factor. MP.2 Reason abstractly and quantitatively.

Facilitation Guidance

Launch the problem by giving students a moment to silently notice and think about the situation, then invite them to jot down questions they could answer mathematically. Encourage them to consider both real-life and map distances, and any assumptions that might be necessary. After a few minutes, have students pair up to share their questions and discuss which ones are most interesting or answerable. Circulate to listen for reasoning, language use, and mathematical clarity.
- Share out as a class. Discuss which questions are answerable with the information given, which questions are mathematical and connected to proportional reasoning and scale, etc.
- Co-craft a list of precise, well-defined questions as a class that are directly connected to the scale context. These questions can be used for Part (b).
Move students back into partner or group work to choose two questions and complete the rest of the work. Expect multiple strategies for Parts (b) and (c): some students may convert the scale to 1 inch = 80 feet, others may repeatedly apply the ¼ inch using quantitative reasoning, and others may use a model, proportion, equation, or other tool. Ask questions such as:
- How did you decide which operation to use?
- Can you show your work in more than one way?
- Does your answer make sense in both real life and on the map?
Debrief the problem by having students showcase their work. Encourage students to reference familiar spaces in the school or neighborhood as they reason about distances, centering their perspectives in the math CRMT Culturally Responsive Math Teaching . Compare the map and real-life distances, emphasizing the underlie proportional relationships. Invite discussion:
- Why is it important to use scale carefully? What are easy mistakes that students might make when using scale?
- How can you use benchmark values and estimation to check the reasonableness of your answers?
- What strategies did you prefer for this problem, and why?

Fishtank Learning

7th Grade Math
Unit 5: Percent and Scaling
Lesson 15

Objective

Warm Up

Anchor Problems - Problem 1

Anchor Problems - Problem 2

Anchor Problems - Problem 3

Problem Set

Target Task

Fishtank Learning

7th Grade MathUnit 5: Percent and ScalingLesson 15

Objective

Warm Up

Anchor Problems - Problem 1

Anchor Problems - Problem 2

Anchor Problems - Problem 3

Problem Set

Target Task

7th Grade Math
Unit 5: Percent and Scaling
Lesson 15